PCA in Action: From Commodities to Trading

Introduction: The Power of Principal Component Analysis

Principal Component Analysis (PCA) is a statistical technique used to reduce data dimensionality while preserving key information. In financial markets, PCA is instrumental in extracting dominant risk factors from complex datasets, making it invaluable for:

✔ Commodity derivatives pricing: Identifying key market drivers

✔ Dispersion trading: Decomposing index volatility into constituent stock volatilities

Figure 1: PCA variance explained in commodity markets

PCA in Commodity Derivatives Pricing

Commodity derivatives are widely used for risk management. PCA helps identify principal factors influencing prices:

- Macroeconomic indicators (inflation, GDP growth, rates)

- Supply/demand shocks (weather, geopolitics)

- Energy prices (oil/gas correlations)

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import yfinance as yf
from sklearn.decomposition import PCA

# Descargar datos de precios históricos de commodities desde Yahoo Finance
tickers = ["GC=F", "CL=F", "SI=F", "HG=F", "ZC=F"]  # Oro, petróleo crudo, plata, cobre y maíz
data = yf.download(tickers, start="2023-01-01", end="2024-01-01")

# Verificar si 'Close' está en los datos
data = data.get('Close')
if data is None:
    raise ValueError("No se encontraron datos de 'Close' en la descarga de Yahoo Finance.")

# Eliminar filas con valores NaN
data.dropna(inplace=True)

# Aplicar PCA
pca = PCA()
pca.fit(data)
explained_variance = pca.explained_variance_ratio_

# Graficar la varianza explicada con mejor claridad
plt.figure(figsize=(8, 5))
sns.barplot(x=np.arange(1, len(explained_variance) + 1), y=explained_variance * 100, palette='viridis')
plt.xlabel('Componente Principal (PCA)')
plt.ylabel('Varianza Explicada (%)')
plt.title('Varianza Explicada por Cada Componente Principal')
plt.xticks(np.arange(len(explained_variance)), labels=[f'PC{i+1}' for i in range(len(explained_variance))])
plt.show()

# Graficar los coeficientes de los primeros 3 componentes principales con escalado para mejorar la interpretación
plt.figure(figsize=(8, 5))
indices = np.arange(len(tickers))
colors = ['b', 'g', 'r']

for i in range(3):
    plt.plot(indices, pca.components_[i] / np.max(np.abs(pca.components_[i])), marker='o', linestyle='-', label=f'PC{i+1}', color=colors[i])

plt.xticks(indices, tickers, rotation=45)
plt.xlabel('Commodities')
plt.ylabel('Peso Normalizado')
plt.title('Pesos Normalizados de las Primeras 3 Componentes Principales')
plt.legend()
plt.show()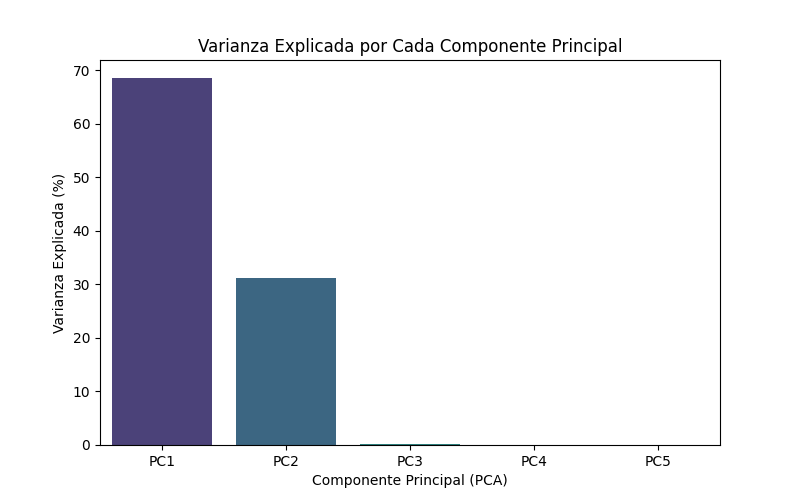

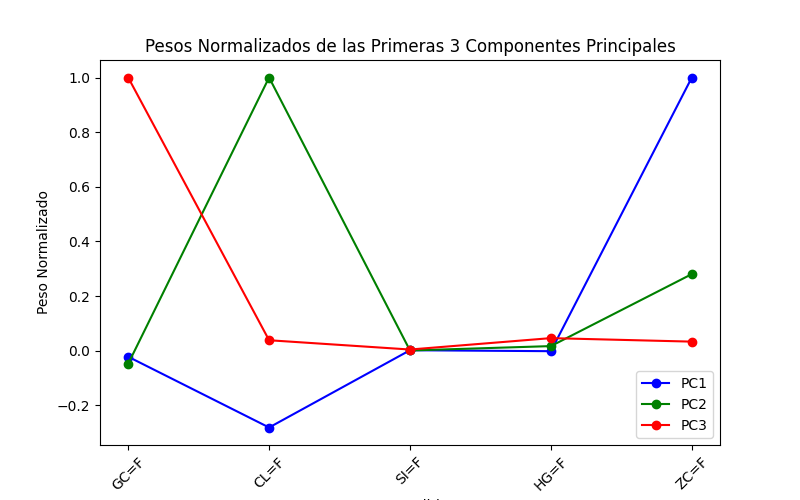
Key PCA Insights

1. PC1 (captures the highest variance): Broad macroeconomic influences

2. PC2: Sector-specific factors

3. PC3: Idiosyncratic shocks

4. PC4+ (minor variance): Additional noise or less significant patterns

The analysis considered multiple principal components, with the first three explaining most of the variance. However, up to five components were visualized for a better understanding of the data structure.

PCA for Dispersion Trading

Dispersion trading exploits differences between index and single-stock volatilities. PCA helps:

✔ Quantify systematic vs. idiosyncratic risk

✔ Identify mispriced volatility components

✔ Optimize hedging ratios

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import yfinance as yf
from sklearn.decomposition import PCA

# Descargar datos de precios históricos de acciones del índice S&P 500 desde Yahoo Finance
tickers = ["AAPL", "MSFT", "GOOGL", "AMZN", "META", "TSLA", "NVDA", "BRK-B", "JPM", "V"]
data = yf.download(tickers, start="2023-01-01", end="2024-01-01")

# Verificar si 'Close' está en los datos
data = data.get('Close')
if data is None:
    raise ValueError("No se encontraron datos de 'Close' en la descarga de Yahoo Finance.")

# Eliminar filas con valores NaN
data.dropna(inplace=True)

# Aplicar Rolling PCA con ventana de 90 días
window_size = 90
pca_results = []
dates = []

for i in range(len(data) - window_size + 1):
    window_data = data.iloc[i:i + window_size]
    pca = PCA()
    pca.fit(window_data)
    pca_results.append(pca.explained_variance_ratio_[:3])
    dates.append(data.index[i + window_size - 1])

# Convertir resultados en array para graficar
pca_results = np.array(pca_results)

# Graficar la evolución de los primeros 3 componentes
plt.figure(figsize=(10, 5))
plt.plot(dates, pca_results[:, 0], label='PC1 - Systematic Risk', color='b')
plt.plot(dates, pca_results[:, 1], label='PC2 - Sector-Specific', color='g')
plt.plot(dates, pca_results[:, 2], label='PC3 - Idiosyncratic', color='r')
plt.xlabel('Fecha')
plt.ylabel('Varianza Explicada')
plt.title('Evolución Temporal de los Primeros 3 Componentes Principales')
plt.legend()
plt.show()

# Obtener pesos de la primera componente principal (PC1) como hedge ratio
pca = PCA()
pca.fit(data)
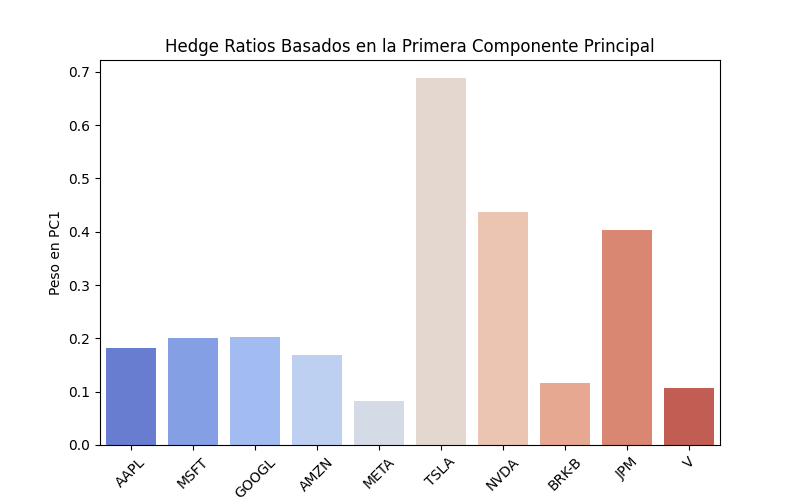
hedge_ratios = pca.components_[0]

# Graficar los hedge ratios
plt.figure(figsize=(8, 5))
sns.barplot(x=tickers, y=hedge_ratios, palette='coolwarm')
plt.xlabel('Acciones')
plt.ylabel('Peso en PC1')
plt.title('Hedge Ratios Basados en la Primera Componente Principal')
plt.xticks(rotation=45)
plt.show()

Practical Applications

1. Rolling PCA windows (60-90 days) for dynamic factor exposure

2. PC1 as hedge ratio for index products

3. Idiosyncratic components for pair trading opportunities

Conclusion

PCA provides a robust framework for identifying market drivers in both commodity pricing and dispersion trading. By decomposing volatility into systematic and idiosyncratic components, traders can develop more effective risk models and capture alpha opportunities.